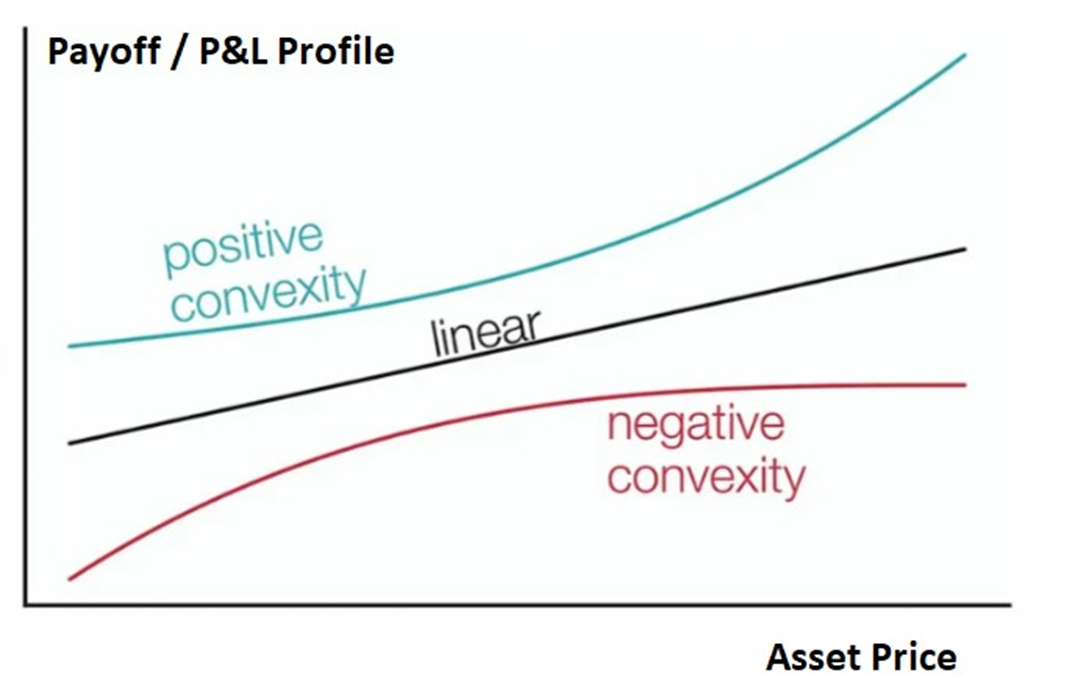
What is a Linear Payoff? What is a Positively or Negatively Convex Payoff?

Linear Payoffs

In Trading & Investing, a linear payoff refers to a financial instrument or investment strategy where the return or payoff is directly proportional to the change in the underlying asset's price. In other words, the payoff exhibits a linear relationship with the movement in the price of the underlying asset.

Linear payoffs are straightforward and follow a linear function. If the value of the underlying asset increases or decreases by a certain amount, the payoff of the investment also increases or decreases by a proportional amount. This linear relationship can be represented by a straight line on a graph (usually a 45-degree line). Examples of linear payoffs include stocks, future or forward contracts on stocks.

Positively Convex Payoffs (Positive Convexity)

A positively convex payoff refers to a type of payoff structure where the rate of increase in the payoff accelerates as the value of the underlying asset or market factor moves in a favorable direction. In other words, the payoff exhibits convexity with a positive curvature. Positively convex payoffs are valuable for investors because they provide the potential for increasing returns in favorable market conditions. Examples include Options or complex combinations of options that exhibit convex behavior in various market conditions.

Negatively Convex Payoffs (Negative Convexity)

A negatively convex payoff refers to a type of payoff structure where the rate of increase in the payoff decelerates as the value of the underlying asset or market factor moves in a favorable direction. In other words, the payoff exhibits convexity with a negative curvature. On a graph, this creates a concave shape. Negatively convex payoffs are important to understand because they impact the risk and return profiles of various investment strategies. Examples include callable bonds and mortgage-backed securities.