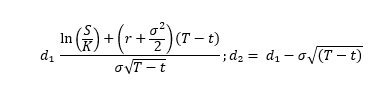Call / Put Options & Black-Scholes Model

Options are financial derivatives that give the holder the right (but not the obligation) to buy or sell an underlying asset at a predetermined price (strike price) within a specified time period. Options are often used for various purposes, including speculation, hedging, and managing risk. They are actively traded in options markets, which are part of the broader derivatives markets.
There are two main types of options: call options and put options.
- Call Option: Gives the holder the right to buy the underlying asset at the strike price before or at the expiration date.
- Put Option: Gives the holder the right to sell the underlying asset at the strike price before or at the expiration date.
What is Volatility? What is the relationship between Volatility and Option Prices? How do we price Options?
Volatility measures the extent of price fluctuations or the degree of risk associated with the price movements of a financial instrument, such as a stock, bond, currency pair, or commodity.
Volatility is typically quantified using statistical measures, with standard deviation being a common method. It represents the average deviation of each data point from the mean (average) of the data set.
Below is an example of a volatile price move (Red) vs a less volatile one (Green):
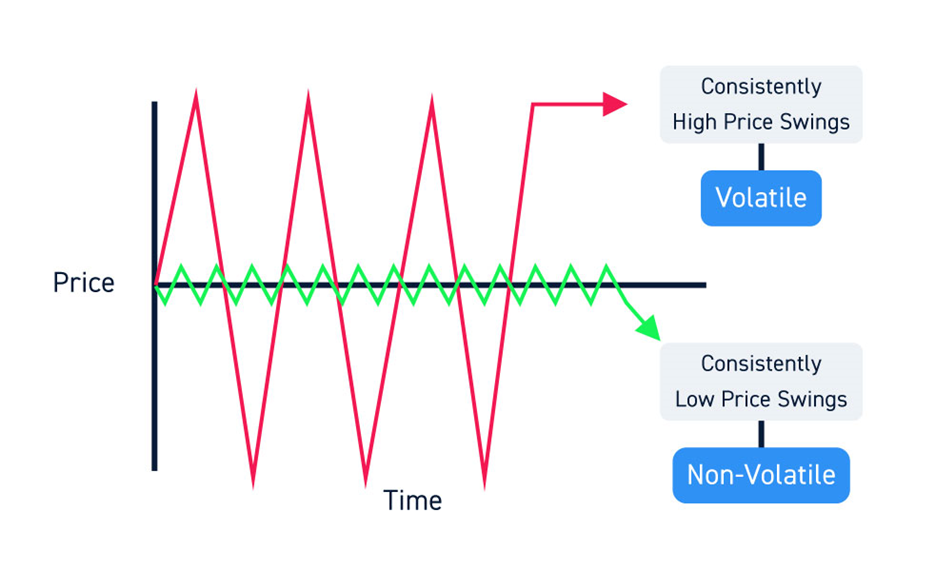
Options are usually priced using the Black-Scholes model or a more complicated iteration of it. Within this model, a higher volatility number that comes into the pricing model leads to a higher option price (the price is also called a premium). That intuitively makes sense: if an asset has higher volatility, it is inherently “riskier”, moves more, and can get to higher / lower price levels, increasing the probability that our call or put option will be monetizable. Hence the call / put option must cost more to account for that.
For reference, below are the Black-Scholes formulas for the prices of a Call and a Put option. This is the most important formula in financial markets!
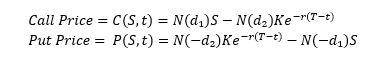
Where:
- S is the current stock price
- K is the option's strike price
- r is the risk-free interest rate
- σ is the volatility of the underlying asset
- T is the option's time to expiration
- t is the current time
- N (⋅) is the cumulative distribution function of the standard normal distribution