What is an Interest Rate Swap?

An Interest Rate Swap (IRS) is a financial derivative contract between two parties that involves the exchange of interest rate cash flows over a specified period. In an interest rate swap, the two parties agree to exchange interest payments in order to manage or hedge exposure to interest rate fluctuations. This type of derivative allows entities to customize their interest rate profiles and effectively manage their interest rate risk.

The most common form of an interest rate swap involves exchanging fixed-rate interest payments for floating-rate interest payments or vice versa. There are two main legs in an interest rate swap:

·         Fixed Leg: One party agrees to pay a fixed interest rate on a notional principal amount over the life of the swap. The fixed interest rate is predetermined at the initiation of the swap and remains constant throughout the swap's term.

·         Floating Leg: The other party agrees to pay a variable (floating) interest rate based on a reference interest rate index, such as the London Interbank Offered Rate (LIBOR) or the Euro Interbank Offered Rate (EURIBOR). The floating rate is reset periodically according to the terms of the swap agreement.

The key features of an Interest Rate Swap include:

·         Notional Principal Amount: The notional principal amount is the hypothetical amount used to calculate interest payments but is not actually exchanged between the parties. It determines the cash flow amounts but does not represent a debt or asset.

·         Payment Frequency: Interest rate swaps can have different payment frequencies for the fixed and floating legs, such as quarterly, semi-annually, or annually.

·         Maturity Date: The maturity date is the agreed-upon date when the interest rate swap contract terminates, and any final settlement occurs.

Interest rate swaps are commonly used for various purposes, including:

·         Interest Rate Risk Management: Entities use interest rate swaps to manage exposure to interest rate fluctuations. For example, a borrower with a variable-rate loan may enter into an interest rate swap to convert the variable-rate payments into fixed-rate payments.

·         Speculation: Traders may use interest rate swaps to speculate on the direction of interest rates, hoping to benefit from favorable rate movements.

·         Asset-Liability Management: Financial institutions use interest rate swaps to align the interest rate characteristics of their assets and liabilities, reducing interest rate risk.

·         Customization: Interest rate swaps offer flexibility, allowing parties to customize their interest rate exposure to meet specific financial goals or requirements.

The valuation of an interest rate swap involves calculating the present value of future cash flows exchanged between the two parties.

The formula for the present value of the fixed leg of an interest rate swap (assuming fixed-rate payments) is as follows:

The formula calculates the present value of each fixed interest payment over the life of the swap, discounted at the swap rate. The sum of these present values represents the total present value of the fixed leg.

For the floating leg (assuming payments are based on a reference rate plus a spread), the present value formula is more complex due to the variability in the cash flows. It involves projecting future cash flows based on expected future reference rates and discounting them to their present value. The formula for the present value of the floating leg can be expressed as:

In practice, traders and financial analysts often use financial software or spreadsheets to perform these calculations. Additionally, the net present value of the swap is the difference between the present values of the fixed and floating legs:

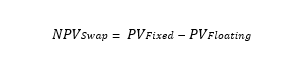
This net present value represents the estimated fair value of the interest rate swap. Keep in mind that these formulas simplify the calculations, and various factors, such as day-count conventions and payment frequency, may affect the actual valuation.

In conclusion, Interest Rate Swaps are widely used in financial markets and they contribute to the efficient allocation and transfer of risk among market participants.